先日引退した、元プログラミング研究会会長、55代のT_SUM_Uです。名前は「つ↑む→」と読みます。自己紹介はここまで、早速本題に入りましょう。まずは次の画像をご覧ください。

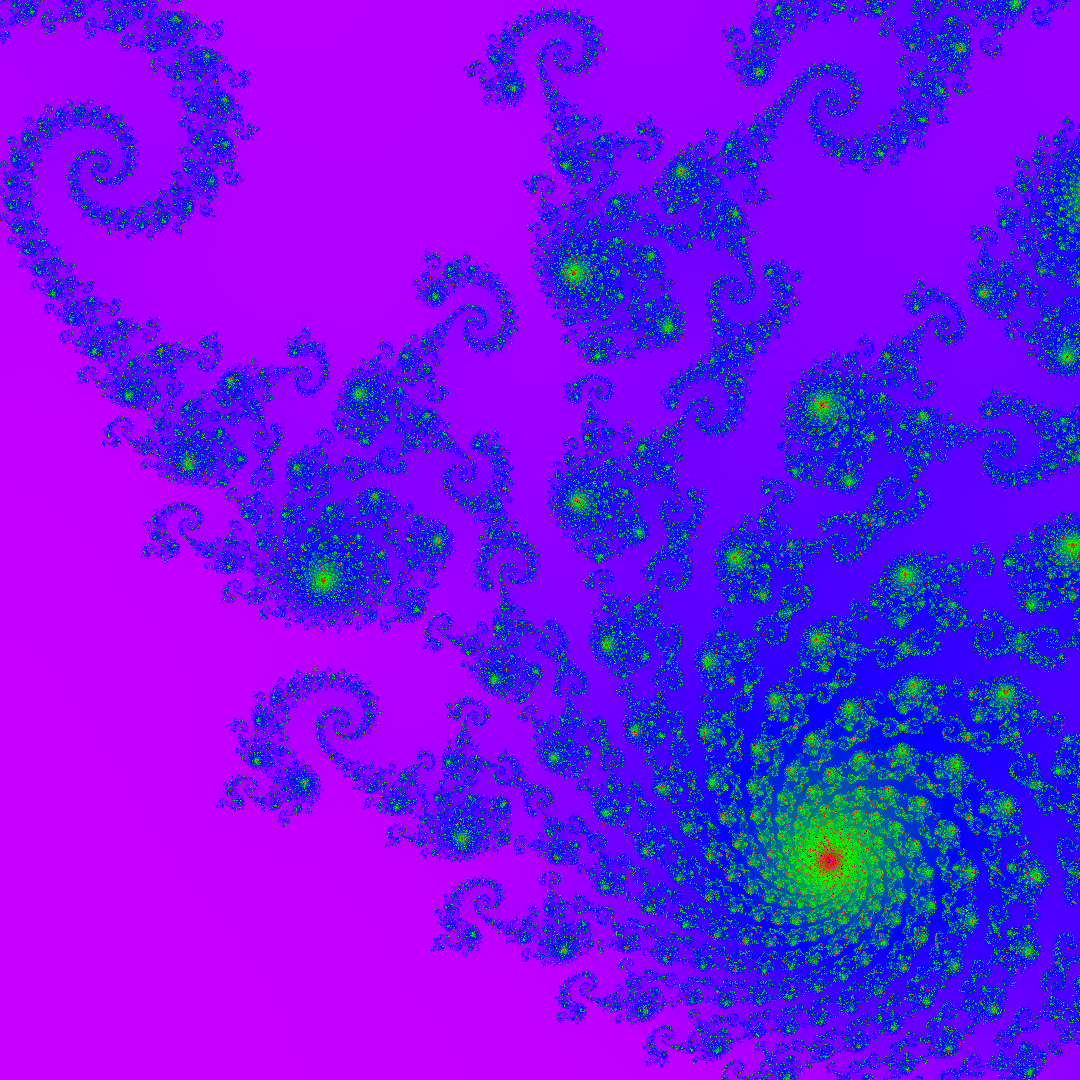
これらの画像はマンデルブロ集合と呼ばれる集合の一部です。このような美しい画像を自分で描けるようになりたくはありませんか？今回はその方法と、ざっくりとした理論を紹介します。

そもそも

「そもそもマンデルブロ集合って何」と思った方も多いと思うので、簡単に説明します。マンデルブロ集合とは、次の式で表される複素数列が ${n \to \infty}$ で無限大に発散しない複素数 $c$ の集合です。

$z_{n+1}={z_n}^2+c$
$z_0=0$

ここで、 $z_n$ も複素数です。ここまで読んだだけで理解できた方はそれほど多くないと思うので、もう少し掘り下げて説明します（この部分は私が以前書いた別の記事と同じ内容です。）。

もう数式を見たくないという方は、ここをクリックして飛ばしてください。

複素数とは二つの実数 $a, b$ と虚数単位 $i=\sqrt{-1}$ を用いて
$z=a+bi$
と表すことができる数です。
この時、 $a$ を実部、 $b$ を虚部と呼びます。複素数を座標平面上に描くときは実部を横軸、虚部を縦軸にとって描きます。
例えば $2+3i$ を描く場合は次の図のようになります。
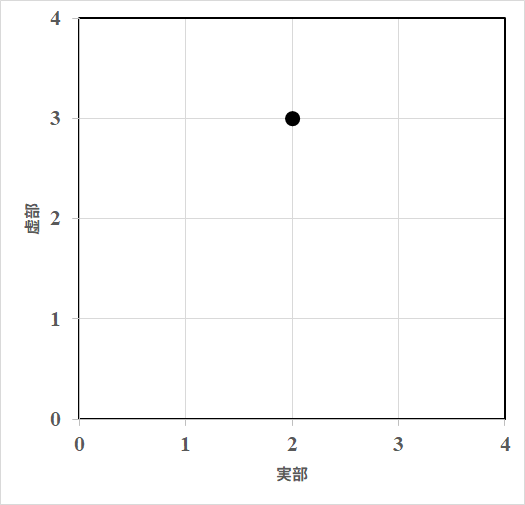
また、この数の大きさは原点との距離となります。つまり、大きさとは次の図に示された線の長さです。

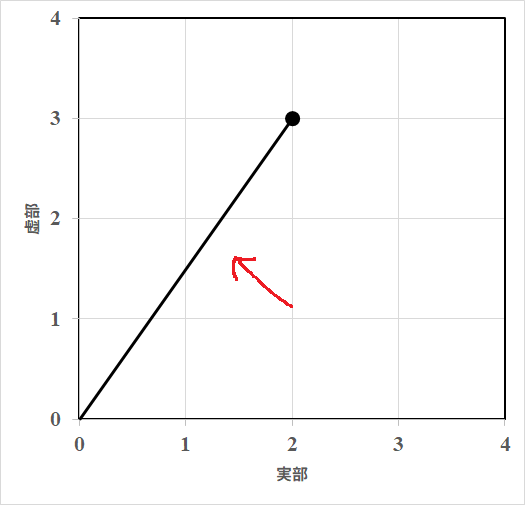
さて、この数を $c$ として上の式に当てはめて計算すると次のようになります。

$z_0=0$
$z_1={z_0}^2+c = {0}^2 + 2+3i = 2+3i$
$z_2={z_1}^2+c={(2+3i)}^2+2+3i=-3+15i$
$.$ $.$ $.$
このようにして $c$ の値を変えて計算していくと、大きさがどんどん大きくなる（無限大に発散する） $c$ と、そうでない $c$ があることがわかります。その中で大きさが無限大に発散しない $c$ のみを描くと、次のような図が出来上がります。

しかし実際には無限回の計算をすることはできないので、計算結果が一定の大きさを超えたら無限大に発散したとみなして描画します。これがマンデルブロ集合の正体でした。着色方法については後程説明します。

つまりどういうこと

簡単にまとめるなら、

計算結果が一定の大きさになるまで同じ式を何度も計算する。

計算結果が一定の大きさになったら、対応する地点に点を打つ

画面が埋まるまでこれを繰り返すと、図形が出来上がる。

ということになります。

描いてみる

それでは実際に描いてみます。Processingを用います。実際に描いてみたいという方はここからProcessingをダウンロードしてください。

ダウンロードしたら次のコードをコピペして実行します。

float x, y, lengthPerPixelx, lengthPerPixely, minx, maxx, miny, maxy, x0, y0;
int limit;
void setup()
{
    x0 = 0;
    y0 = 0;
    
    minx = -2.2;
    maxx = 0.8;
    miny = -1;
    maxy = 1;
    
    limit = 256;    
    size(900, 600);
    colorMode(RGB);
    stroke(255);
    background(0);
    noSmooth();
    
    lengthPerPixelx = (maxx - minx) / width;
    lengthPerPixely = (maxy - miny) / height;
    for (int i = 0; i < width; i++)
    {
        for (int j = 0; j < height; j++)
        {
            float a = i * lengthPerPixelx + minx;
            float b = j * lengthPerPixely + miny;
            float x_, y_;        
            x = x0;
            y = y0;        
            for (int k = 0; k < limit; k++)
            {         
                x_ = (x * x) - (y * y) + a;
                y_ = 2 * x * y + b;                
                if (x_ * x_ + y_ * y_ > 8)
                {
                    point(i, j);
                    break;
                }                
                x = x_;
                y = y_;
            }
        }
    }
}

実行したら次の画像が出力されます。これだけです。簡単でしょう？

着色する

皆さんの仰りたいことはよくわかります。
「色がついていないじゃないか！騙された！」
とでも言いたいのでしょう。ご安心ください。これから説明します。

先程、「計算結果が一定の大きさになるまで同じ式を何度も計算し、対応する地点に点を打つ。」という内容の説明をしたことを覚えていますでしょうか。色を付けるには、「計算結果が一定の大きさになるまでに計算した回数」を用います。この回数のことを、とりあえず計算回数とでも呼ぶことにします。
着色について説明する前に、最大計算回数について触れておきます。例えば、計算結果がいつまでも一定の大きさにならなかったらどうすればよいでしょうか？無限回の計算が必要になってしまいます。しかし無限回の計算はできません。そこで、「計算結果が一定の大きさにならなくても、一定の回数に到達したらそこで計算を打ち切る。しかし、ここでは点は打たない。」という概念を導入します。この回数を「最大計算回数」と呼ぶことにします。先程のコードで生成された画像には白い部分と黒い部分がありますね。白い部分は「計算結果が一定の大きさに達した部分」、黒い部分は「最大計算回数まで計算しても計算結果が一定の大きさに達しなかった部分」です。このコードでは一定の大きさを8、最大計算回数を256回としました。

それではこの最大計算回数を360回にし、計算回数にHSBの色相を割り当ててみます。 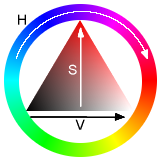[1]
皆さんお馴染みの色相環です。
コードを以下のように書き換えます。

float x, y, lengthPerPixelx, lengthPerPixely, minx, maxx, miny, maxy, x0, y0;
int limit;
void setup()
{
    x0 = 0;
    y0 = 0;
    
    minx = -2.2;
    maxx = 0.8;
    miny = -1;
    maxy = 1;
    
    limit = 360;    
    size(900, 600);
    colorMode(HSB, 360, 100, 100);
    background(0);
    noSmooth();
    
    lengthPerPixelx = (maxx - minx) / width;
    lengthPerPixely = (maxy - miny) / height;
    for (int i = 0; i < width; i++)
    {
        for (int j = 0; j < height; j++)
        {
            float a = i * lengthPerPixelx + minx;
            float b = j * lengthPerPixely + miny;
            float x_, y_;        
            x = x0;
            y = y0;        
            for (int k = 0; k < limit; k++)
            {         
                x_ = (x * x) - (y * y) + a;
                y_ = 2 * x * y + b;                
                if (x_ * x_ + y_ * y_ > 8)
                {
                    stroke(k, 100, 100);
                    point(i, j);
                    break;
                }                
                x = x_;
                y = y_;
            }
        }
    }
}

そして次の画像が出力されます。どうですか？簡単でしょう？

もっと美しく

先程はわかりやすい色のグラデーションとしてHSBの色相を用いましたが、残念ながらこの方法ではなかなか美しい画像は生成できません。実際、先程出力された画像も目が疲れるような画像だったでしょう。ではどうするか。簡単です。HSBがだめならRGBを用います。具体的には、任意の二つのRGBの色を選択し、それを計算回数に応じて線形補完します。

どういうことかというと、つまりこういうことです。そして色を増やします。これをマンデルブロ集合に適用します。コードを書き換えて実行します。

double x, y, lengthPerPixelx, lengthPerPixely, minx, maxx, miny, maxy, x0, y0;
int limit;
int limitScale;
color[] colors;
void setup()
{
    colors = new color[5];
    colors[0] = color(255,0,255);
    colors[1] = color(0,255,0);
    colors[2] = color(0,0,255);
    colors[3] = color(255,255,0);
    colors[4] = color(255,0,0);
  
    x0 = 0;
    y0 = 0;    
    
    minx = -2.2;
    maxx = 0.8;
    miny = -1.5;
    maxy = 1.5;
    
    limitScale = colors.length - 1;
    
    limit = 256 * limitScale;    
    size(1080, 1080);
    colorMode(RGB, 255);
    background(0);
    noSmooth();
  
    lengthPerPixelx = (maxx - minx) / width;
    lengthPerPixely = (maxy - miny) / height;
    for (int i = 0; i < width; i++)
    {
        for (int j = 0; j < height; j++)
        {
            double a = i * lengthPerPixelx + minx;
            double b = j * lengthPerPixely + miny;
            double x_, y_;        
            x = x0;
            y = y0;        
            for (int k = 0; k < limit; k++)
            {         
                x_ = (x * x) - (y * y) + a;
                y_ = 2 * x * y + b;                
                if (x_ * x_ + y_ * y_ > 1000)
                {
                    Colorize(k);
                    point(i, height - j - 1);
                    break;
                }                
                x = x_;
                y = y_;
            }
        }
    }
    save("0.png");
}

void Colorize(int k)
{
  int q = (k / 256) % limitScale; //q is quotient
  int m = k % 256; //m is modulo
  stroke(lerpColor(colors[q], colors[q + 1],(float)m / 256));
}

次の画像が生成されます。コード冒頭部分の色の配列の値を変えれば任意の色のマンデルブロ集合が描けます。簡単でしょう？

拡大

しかし皆さんはまだ疑問を抱いているはずです。
「冒頭の画像と形が違うではないか。」
これから説明します。なんとマンデルブロ集合は無限に拡大できます。より正確に言うと、どれだけ拡大しても次々と図形が出てきます。
これは実際に見てみるのが最もわかりやすいです。 www.youtube.com ちなみにこの動画は私がProcessingで作りました。
つまり、うまく拡大しうまく着色するとこの記事冒頭のような画像が生成できるわけです。これまでこの記事で紹介したコードでは全てコードの冒頭部分で描画する範囲を指定しています。

    minx = -2.2;
    maxx = 0.8;
    miny = -1.5;
    maxy = 1.5;

の部分です。これまで生成した画像は横方向に-2.2~0.8、縦方向に-1.5~1.5の範囲で描画をしていたということになります。
それでは仮に横方向に-0.71234708353~-0.71134708353、縦方向に0.24613349671~0.24713349671の範囲で描画してみます。着色方法は先程と同じです。実に簡単です。

拡大方法

しかしまだ皆さんは言いたいことがあることでしょう。
「そんな描画範囲は一体どうやって見つけたのか」と。私はこれまでに2つの方法を試してきました。それを紹介します。

最大差分法

各分割部分の各ピクセルの計算回数の最大値と最小値の差をとり、最も差が大きい分割部分を選択して拡大します。この方法だと、マンデルブロ集合の先端部分（次の図に示した部分）が主に選択されて拡大されます。計算回数の差の最大値を持つ分割部分を選択することから、最大差分法（Max Gap、MG法）と名付けました。
この方法を用いて拡大すると次の動画の通りになります。 www.youtube.com

まだ試したことがない方法

最大差分法の逆で、各分割部分の計算回数の最大値と最小値の差が最も小さい部分を選択して拡大する方法はまだ試していません。この方法では、差が0の部分は図形の内側なので除外します。

また、分割部分のうち最大計算回数に達したピクセルとそうでないピクセルの両方を含む部分を選択して拡大する方式も考えました。これもまだ試していませんが、おそらくこれが最も面白いのではないかと思います。

おわり

長い記事でしたが、お楽しみいただけたでしょうか？記事の内容に関する質問などはTwitterまでお願いします。
最後に私事ですが、これをもって私のMIS.Wでの活動は終わりとなります。2022年公式アドベントカレンダーの最終日を担当できたことを光栄に思います。MIS.Wの先輩方、所属する各位、そしてアドベントカレンダー係の56代だんご仙人さんに感謝申し上げます。

本日はクリスマス、今年も残り1週間を切りました。本記事で紹介した美しいマンデルブロ集合と共に、良いクリスマスと良い新年をお過ごしください。それではさようなら。