新歓ブログリレーの概要と数学が苦手でもわかるマンデルブロ集合【新歓ブログリレー2022 0日目】

MIS.W新歓ブログリレーへようこそ！55代（3年生）のT_SUM_Uです。この記事は新歓ブログリレー0日目とのことで、ここではまず新歓ブログリレーとは何なのかを説明しようと思います。
新歓ブログリレーとは、MIS.W創設記念日である4月16日を最終日として、サークル員が毎日記事を投稿していくイベントです。内容はサークル活動（プログラミング、CG、DTMなど）、大学生活など様々ですが、完全に執筆者に任せているので、明日がどんな内容になるのかすら私にもわかりません。どんな内容の記事が来るのか楽しみですね！
このブログリレーを通してMIS.Wやその活動内容に興味を持っていただけたら幸いです。興味を持っていただけましたら、是非とも公式Twitterまで！ twitter.com

数学が苦手でもわかるマンデルブロ集合

さて、この記事はブログリレーの0日目、つまり本来はブログリレー開始の挨拶をする場なのですが、それだけだとつまらないので付録を付けておきました。ここではマンデルブロ集合を描きます。そもそもマンデルブロ集合はご存じでしょうか？こちらがマンデルブロ集合です。 見たことはあるという方も多いのではないでしょうか。
この図形は次の式で表される複素数列がで無限大に発散しない複素数の集合です。

ここで、も複素数です。この時点で何を言っているのかわからないという方もいると思うので簡単に説明しましょう。
まず、複素数とは二つの実数と虚数単位を用いて

と表すことができる数です。
この時、を実部、を虚部と呼びます。 複素数を座標平面上に描くときは実部を横軸、虚部を縦軸にとって描きます。
例えばを描く場合は次の図のようになります。
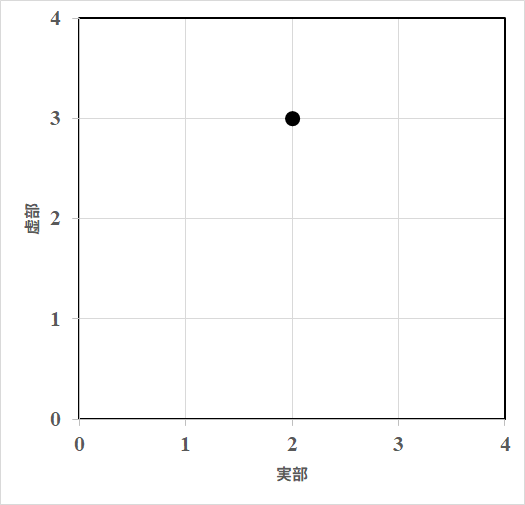
また、この数の大きさは原点との距離となります。つまり、大きさとは次の図に示された線の長さです。

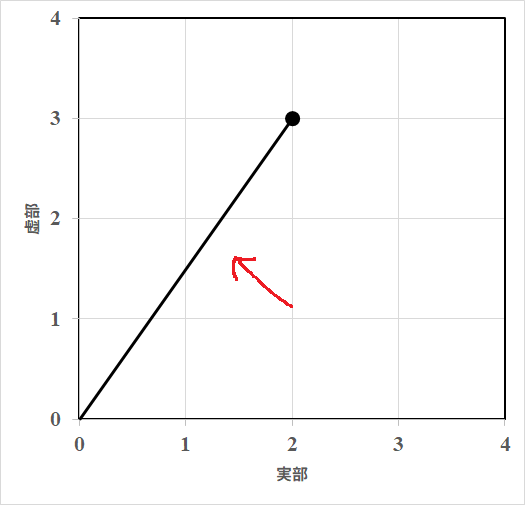
さて、この数をとして上の式に当てはめて計算すると次のようになります。

このようにしての値を変えて計算していくと、大きさがどんどん大きくなる（無限大に発散する）と、そうでないがあることがわかります。その中で大きさが無限大に発散しないのみを描くと、次のような図が出来上がります。

実部の範囲:[-2.2, 0.8]、虚部の範囲:[-1, 1]

これがマンデルブロ集合の正体でした。

色

ここまで読んでこう思った方もいらっしゃるでしょう。
「色は？」
先程述べた通り、マンデルブロ集合は点の集まりです。なので、本来色はありません。しかしそれだと面白くないので、わざと着色をしているわけです。
これには様々な方法がありますが、この記事の最初の画像では発散の速さによって着色をしています。本来は無限回の計算をしなければならないのですが、実際はそうもいかないので、有限回の計算で大きさがある値を超えたら無限大に発散するとみなして描きます。大きさがある値を超えたとき、計算回数が少なければ少ないほど発散が速いということになります。その計算回数に応じた色を付けることで最初の画像が出来上がるわけです（気づいているかもしれませんが、この場合は無限大に発散する点を描画しています）。

終わり

最後に記事の最初に貼ったマンデルブロ集合を描くプログラムを掲載してこの記事を締め括ります。最後まで読んでいただきありがとうございました！
次は55代のUSNLさんによる記事です。
https://misw.hatenablog.com/entry/2022/04/04/000000

使用環境:Processing 4.0b2

float x, y, lengthPerPixelx, lengthPerPixely, minx, maxx, miny, maxy, x0, y0;
int limit;
void setup()
{
    x0 = 0;
    y0 = 0;
    
    minx = -2.2;
    maxx = 0.8;
    miny = -1;
    maxy = 1;
    
    limit = 360;    
    size(1500, 1000);
    colorMode(HSB, 360, 100, 100);
    background(0);
    
    lengthPerPixelx = (maxx - minx) / width;
    lengthPerPixely = (maxy - miny) / height;
    for (int i = 0; i < width; i++)
    {
        for (int j = 0; j < height; j++)
        {
            float a = j * lengthPerPixely + miny;
            float b = i * lengthPerPixelx + minx;
            float x_, y_;        
            x = x0;
            y = y0;        
            for (int k = 0; k < limit; k++)
            {            
                x_ = (x * x) - (y * y) + b;
                y_ = 2 * x * y + a;                
                if (x_ * x_ + y_ * y_ > 1000)
                {
                    stroke(k, 100, 100);
                    point(i, j);
                    break;
                }                
                x = x_;
                y = y_;
            }
        }
    }
}