MIS.W51代プログラム研究会に所属しているikaros(Twitter:ikarostech)です。
MIS.Wに所属しながらFluid-Structure Interaction(FSI)の研究をしています。
今回はその中でも構造つまり、いかに構造物が破綻しないように設計するか簡単な事例を交えながらお話していきたいと思います。
・Finite Element Method(FEM、有限要素法)とは
さて、構造物の評価を行う際、普遍的な評価モデルとは何でしょうか。
構造物においては空力モデルとはことなりミクロな観点からマクロな指標を得る手法が用いられます。
その中の一つがFinnite Element Method(FEM、有限要素法)です。
FEMは構造物を微細なメッシュに分割しそのメッシュ領域内外で働く応力を計算することで構造物全体の評価をおこなう方法です。力学的観点からいえば微小領域に区切りそれを積分しているといえばわかりやすいでしょうか。
この際、用いられるメッシュは多種あり、用途によってさまざまな区切り方があります。代表的なものに3次元構造物に対して六面体メッシュを用いたり、線状構造物に長方形(台形)メッシュが用いられています。
FEMは構造解析モデルとして用いられるだけでなくFSI解析、熱伝熱解析など汎用性の高い解析モデルとして様々な用途に使われています。

図1. COMSOLによるFEMを用いたFSI解析
・構造材に働く力、応力について
さて話を戻して構造材に働く材料力学的作用について考えましょう。
高校物理や大学の基礎力学においては例外を除いて剛体、つまり力をかけても変形したり破壊したりしない物体のみを扱います。
一方で実際の材料は考えていただければお分かりだと思いますが、力をかければしなったり、折れたり、縮んだり…様々な挙動を示します。
材料力学における材料を変形、破壊をさせる物理量のことを応力(Stress)とよび単位は力[N]ではなく圧力[Pa]を用いて表現します。
主な応力には以下のようなものがあります。
・圧縮/引っ張り応力
・せん断応力
・ねじり応力
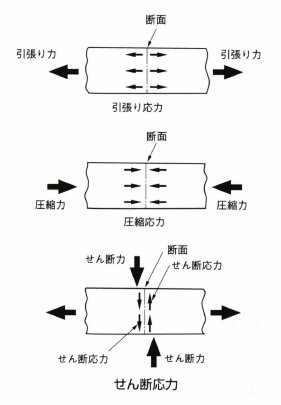
図2. 各応力の概略図[1]
・曲げ応力
などなど
FEMにおいてはこれらの応力をせん断応力が0になるように座標系をとって応力を計算します。この時求められた応力を「主応力」と呼びそれを持ちいて構造物を評価していきます。
・構造解析の実践
では実際に簡単なFEMを実装してみましょう。
と言いたいところなのですが、実際のFEMは組むための前提知識として、材料力学の知識だったり、「仮想仕事の原理」「最小ポテンシャルエネルギーの原理」など導入しなければならない概念が多いため、今回はFEMではなく各メッシュに対して解析解を求めるFEMもどきを組んでいきます。
今回は構造物評価では最もポピュラーな「片持ち梁への一点集中荷重」の定常状態(物体にかかる力が釣り合って時間変化によって形状が変化しない状態)における「たわみ」についての形状解析を行いたいと思います。
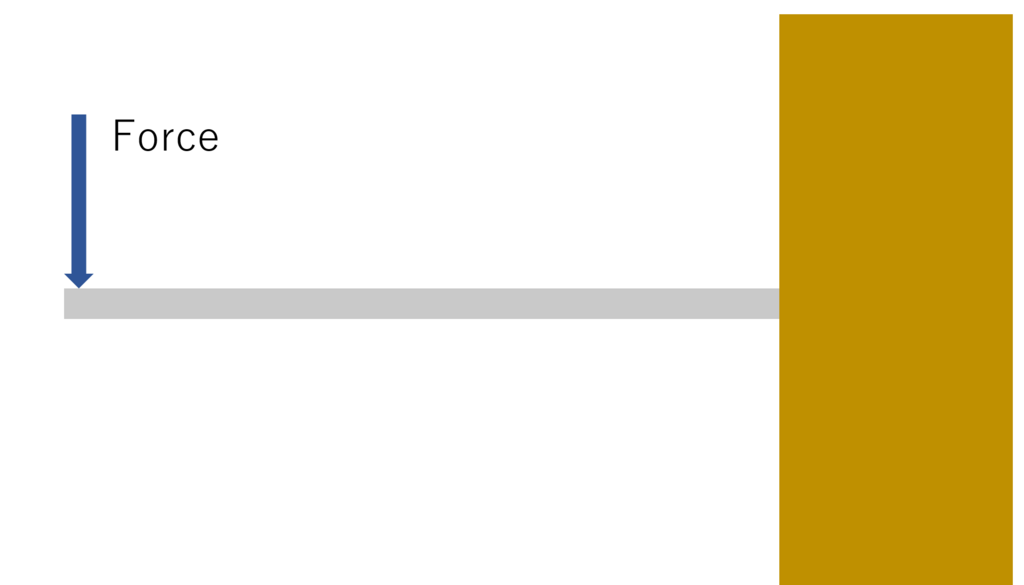
図3.片持ち梁への一点集中荷重
今回はメッシュを等間隔四角形メッシュ、主応力を曲げ応力、梁の自重は無視して計算していきましょう。

図4.片持ち梁への等間隔四角形メッシュの適用
次に曲げモーメントに対する四角形メッシュの挙動を定義してあげます
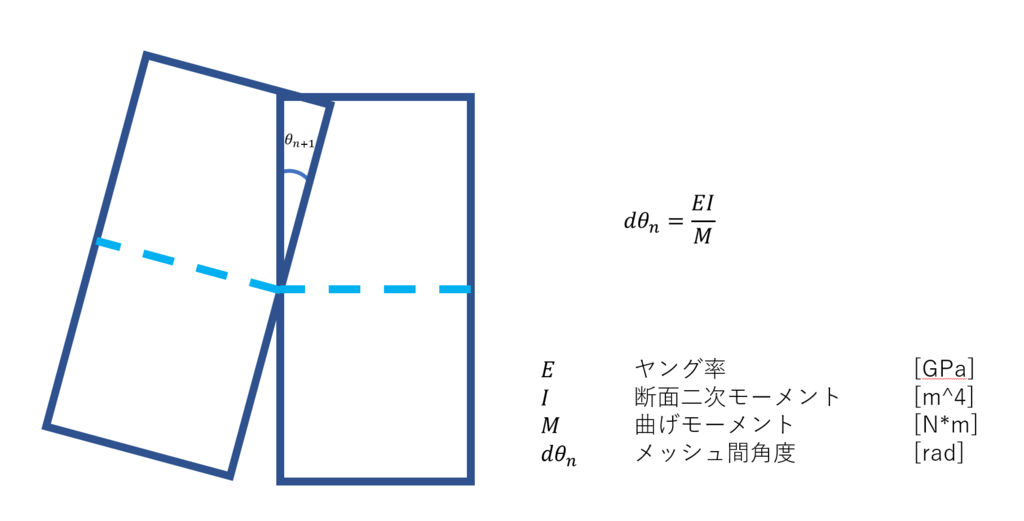
図5.定常時の曲げモーメントと曲率の関係
では解いていきましょう
端に一点集中荷重がかかっている時の各メッシュにかかるモーメントは下の図6のようになります

図6.片持ち梁に対する曲げモーメントの図(下Mの欄)[2]
各メッシュにかかる曲げモーメントはメッシュの位置 xにのみに依存し、荷重がかかっている位置を0、一点集中荷重の大きさをFとすると
曲げモーメントは M=Fx と表されます。
環境は今回はExcelでやっていきましょう。
シート名「マテリアルコンフィグレーション」のB1セルにヤング率と断面二次モーメントの積である曲げ弾性率[Nm2]の値「3000000」(3・10^6 Nm2)を
またB3セルに一点集中荷重の値「294」(294N,30kgf)を入力します。
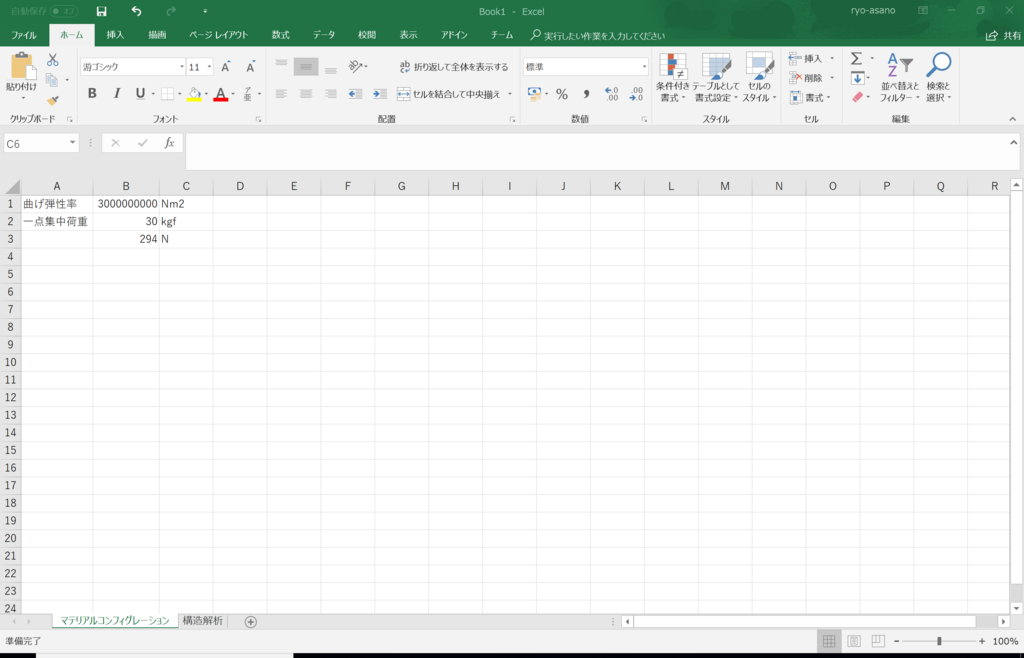
図8.マテリアルコンフィグレーションシート
では構造解析をしてみましょう。片持ち梁の梁の長さは1000 mm、梁の座標系Lは壁に固定されている地点(固定端)を0に、荷重がかかる先端(自由端)を1000にします。
梁にかかる曲げモーメントは梁の座標,lに対して M=294・(1000-l)と求められます。
そこからdθが求められます。
累計でのたわみ角θはdθの累積によって、絶対座標x,yも同様に前のx,y座標から求めることができます
具体的に
となります。
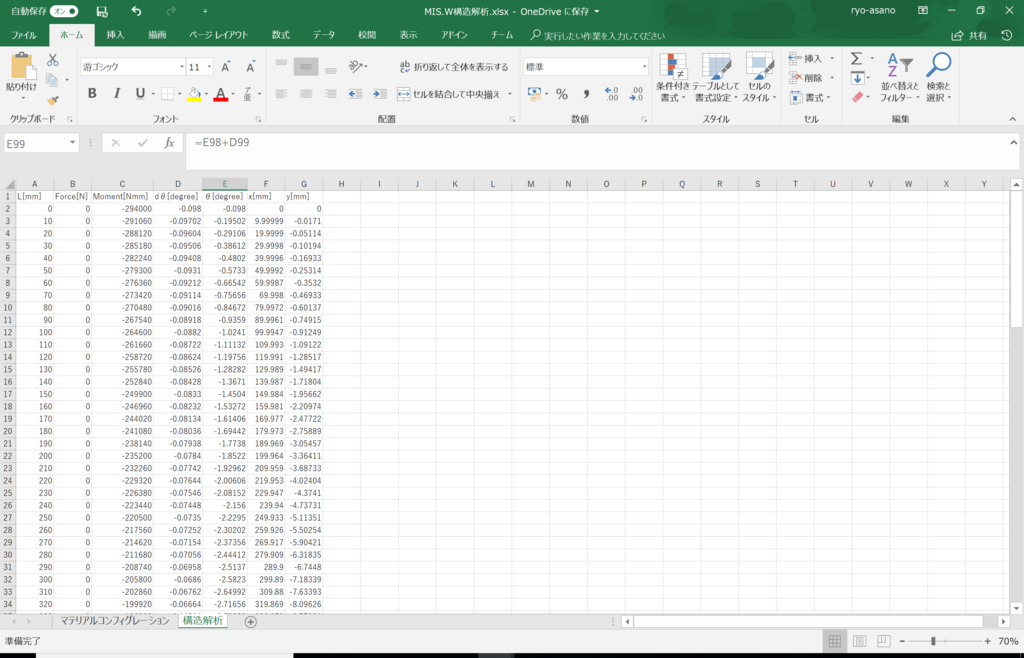
図9. 構造解析シート
ではエクセルに数式を打ち込んでいきましょう。
1行目は表のヘッダーとして使い実際の値は2行目から打ち込んでいきます。
以降断りがない限りエクセルのA列、i行目のセルをを「Aiセル」のように記述します。
エクセルの表は以下の通りに制作します。
| 列 | 内容 | 境界条件 | 記述 |
| A | 梁の座標[mm] | - | Ai=10*(i-1) from A2 to A102 |
| B | 荷重[N] | - | Bi=0 from B2 to B101, B102=294 |
| C | モーメント[N*mm] | 自由端で0 | Ci=B$102*Ai from C2 to C102 |
| D | 曲率[degree] | - | Di=Ci/マテリアルコンフィグレーション!B$1 from D2 to D102 |
| E | たわみ角[degree] | 固定端で0 | E2=0, Ei=E(i-1)+Di from E3 to E102 |
| F | 絶対x座標[mm] | 自由端を0 | F2=0, Fi=F(i-1)+cos(E(i-1)/180*PI()) from E3 to E102 |
| G | 絶対y座標[mm] | 自由端を0 | G2=0, Gi=G(i-1)+sin(E(i-1)/180*PI()) from G3 to G102 |
表1 構造解析シート記述内容
では最後にグラフで可視化してみましょう
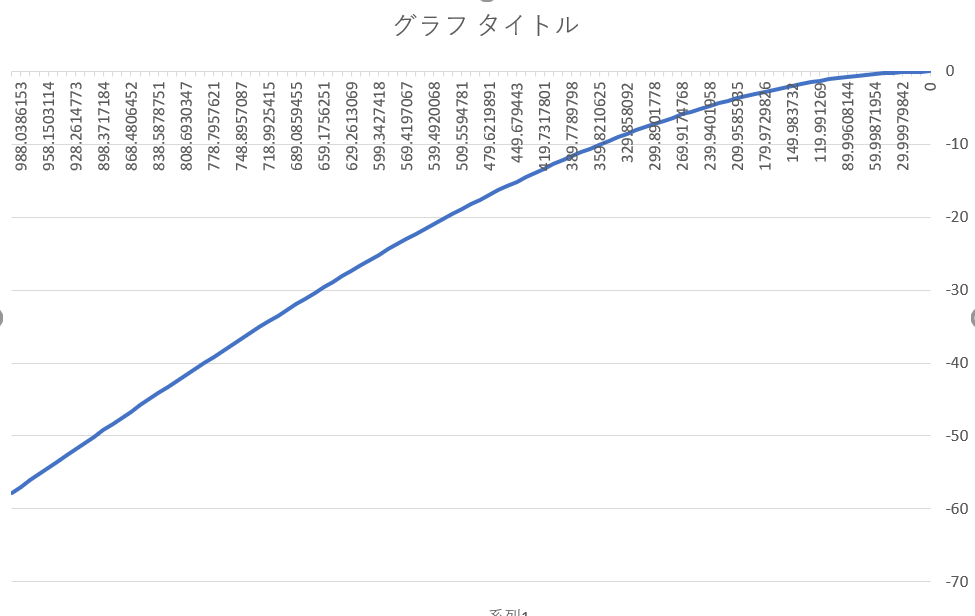
図10.構造解析したたわみ曲線
いかがでしたでしょうか。うまくいかないときは正しい列にデータが入力されているか確認してみてくださいね。また構造解析のエクセルはこちらにも公開しておきます。参考にしてください。
・構造解析の実際
今回は解析的に定常状態の構造材のたわみ解析を行いました。FEMにおける解析ではこのメッシュ間において非線形の微分方程式を数値計算的に解いていきます。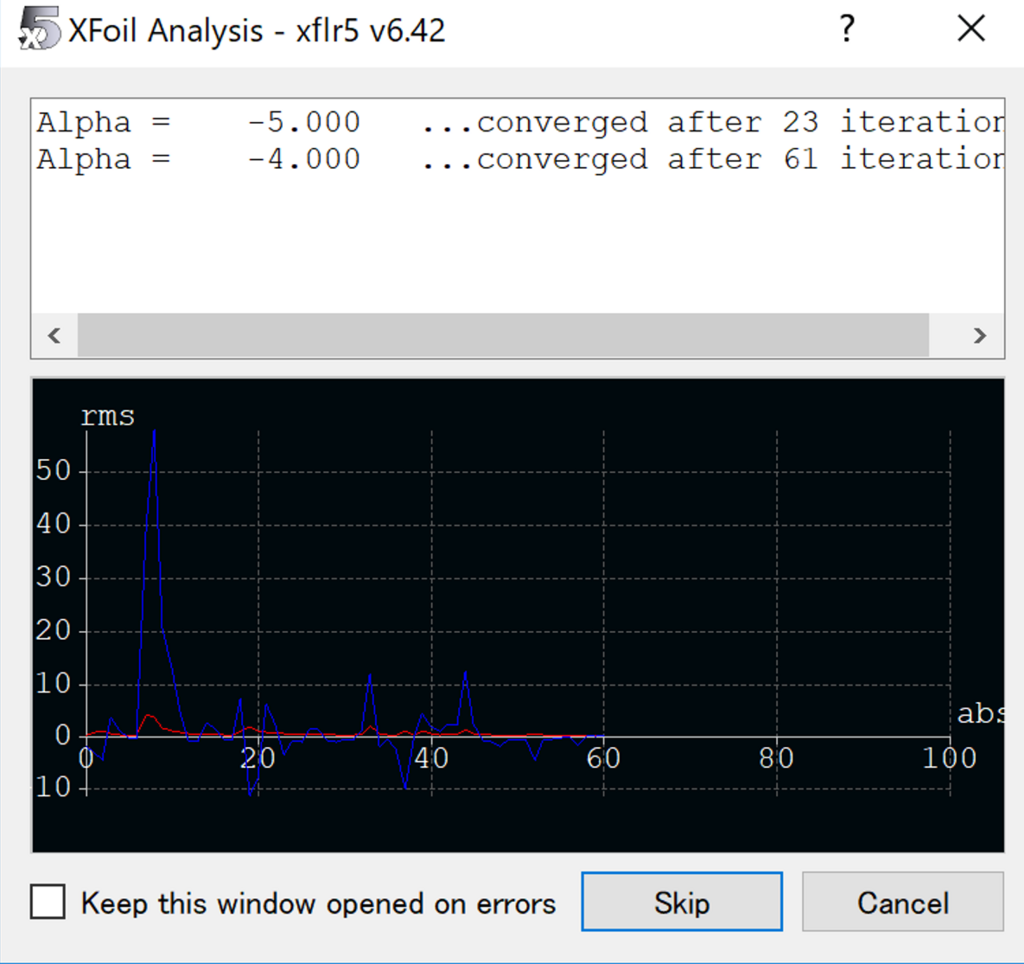
図11
例えば、上図11においてはある流線形状に対して気流を当てた際の圧力分布を求めるFSI解析を行っている時の解析画像です。横軸は反復計算回数、縦軸は収束の度合いを示しています。
流体の解析においては非線形項を含むナビエ=ストークス方程式の近似解を求めることになります。非線形項を含む方程式の求解は適当に初期値をとってそこから拘束条件に当てはめた時のポテンシャルエネルギーとその最小条件とのずれを比較して、最小条件に向かうように値を訂正していくという計算を反復して解いていくことになります。またそれだけに計算のコストも非常に大きいです。
非線形項が出てくるのは流体分野だけでなく、物体の過渡応答について調べる振動工学、伝熱工学、破壊材料力学などありとあらゆる分野にて登場します。*1そのため、この計算コストを精度を保ちながら下げる研究を私は行っています。
またほかにも構造解析には、荷重をかけた時に構造材が折れたり、つぶれたりしないかどうかを解析する「破壊(安全率)解析」、荷重をかけてどのように物体が動くかを解析する「不静定解析」など複数の解析を行って形状を決定していきます。
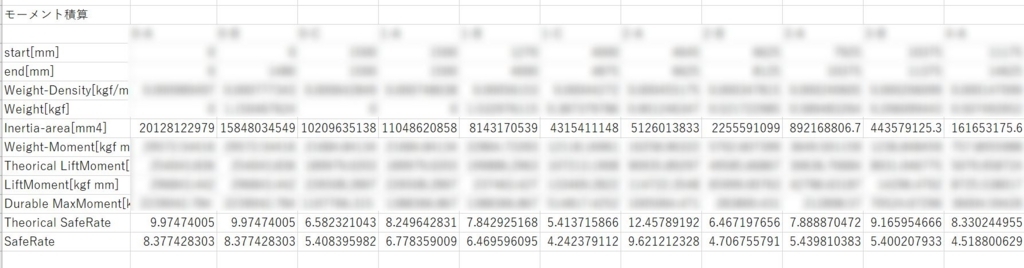
図12 梁の破壊解析
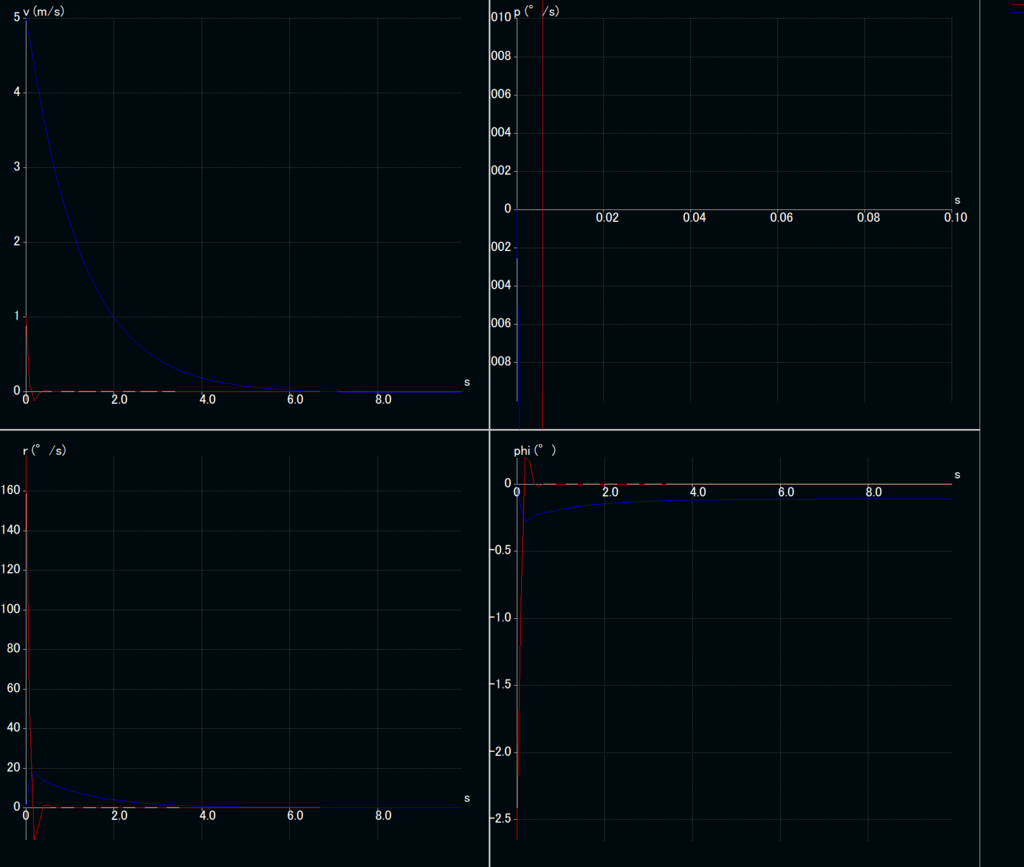
図13 グライダーの運動解析
では構造解析についてまとめます
まとめー構造解析
・構造物を細かく分割し、その分割された部分ごとの計算を行うことで構造を解析できる
・一般に構造解析の計算コストは重い
・構造探索とアルゴリズム
では次に、構造物の形状を決定する構造探索のお話をしましょう。
構造探索では、ある拘束条件のもと、何かあるパラメーターを最小あるいは最大にすることを目標に形状を決定していきます。
では先ほどの片持ち梁の構造探索の例を交えてその解析についてお話したいと思います。
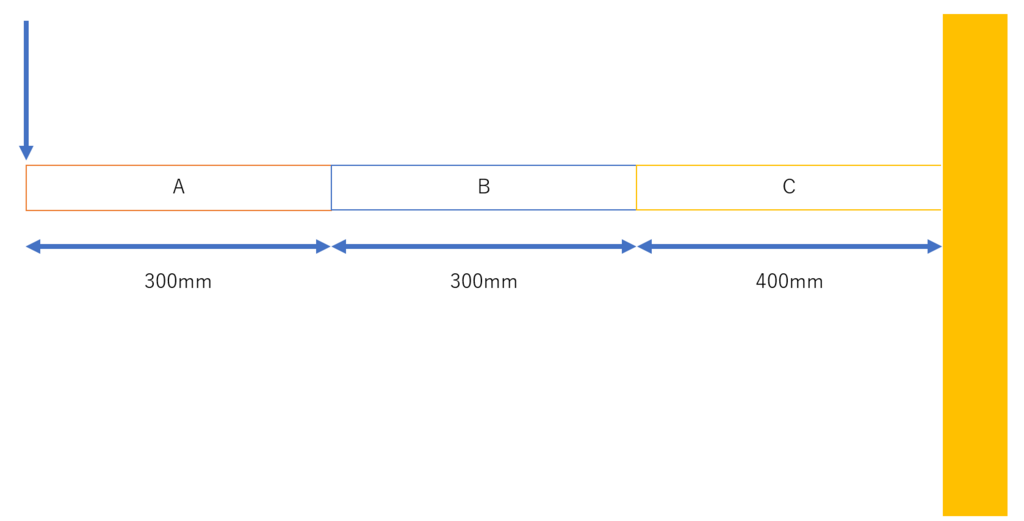
図14 条件付き片持ち梁
| 梁の名前 | 曲げ弾性率[MPa] | 価格[円/mm] |
| α | 1.0 | 2 |
| β | 1.5 | 4 |
| γ | 3.0 | 10 |
表2 梁のコンフィギュレーション
図13のように、A,B,Cの3地点において梁の種類を変えられる片持ち梁が存在し、荷重がAの自由端にかけられている。表2に示す3種類の梁を自由にA,B,Cにつけるとき、たわみ量(自由端におけるy座標の絶対値)が70mmを下回るという条件の下で費用を最小化せよ
さて、つける場所が3か所、梁の種類が3種類ですのでこのケースでは全探索でも求められそうです。
ですが実際にこれが大きくなると手におえないので積極的な枝切りを行うことを考えます。
1.探索木の構成
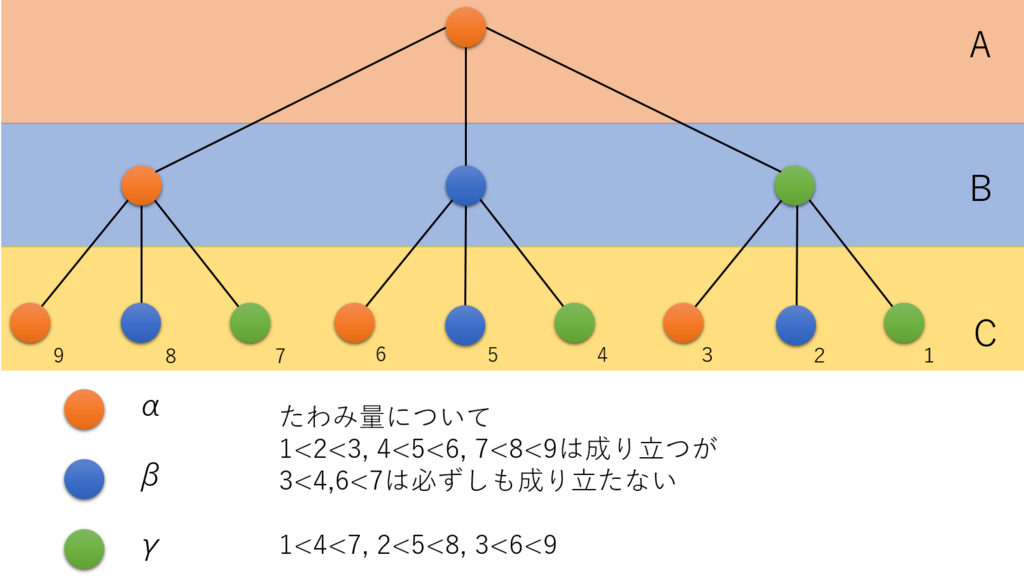
図15 A地点をα梁にした際の探索木
2.探索と枝切り
さて、一般的にたわみ量が小さいと考えられる右側1のノードから計算を始めることを考えます。
このとき枝切りは2パターン考えられます
① 同じ親ノードを持つ子ノードの枝切り
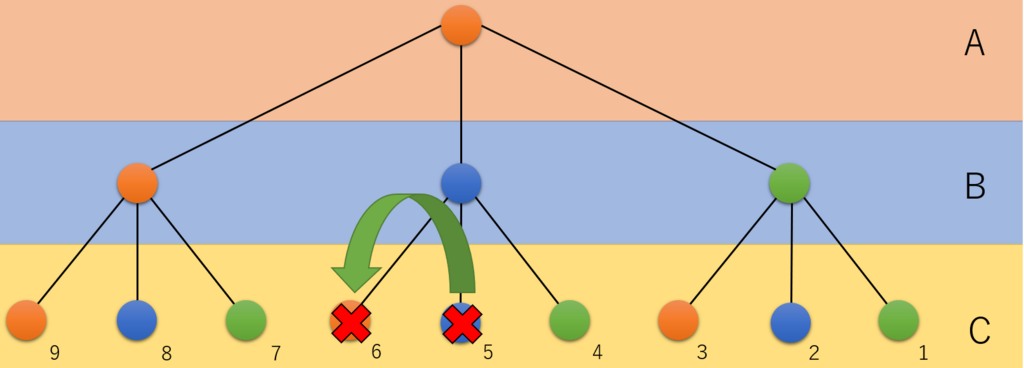
図16 ①パターンの枝切り
図のように5のノードがたわみ量の条件を満たせずたわみ過ぎてしまったとします。
このとき以降の同じ親を持つノードは5のノードよりたわんでしまう、つまり条件を満たせないのでたわみの計算をしなくてもよいということになります。
② 違う親ノードを持つ同じ階層のノードの枝切り
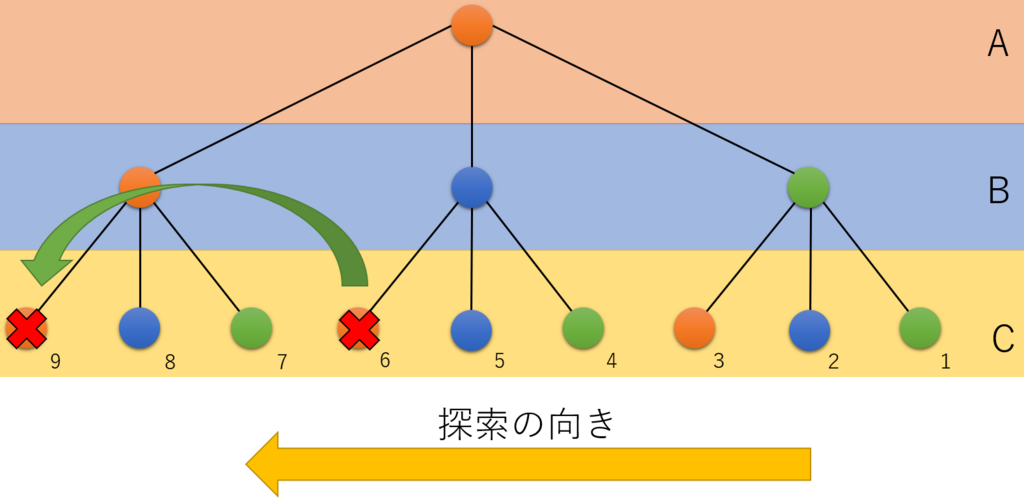
図17 ②パターンの枝切り
図のように6のノードがたわみ量の条件を満たせずたわみ過ぎてしまったとします。
その場合、9のノードは6のノードの時よりたわみ量が大きいのでたわみ計算をしなくてもよいということになります。
3.実装
では実装していきましょう。言語はCを使っていきます。
#define _USE_MATH_DEFINES #include "math.h" //張替えができる梁の種類(A,B,C) const int Level = 3; //梁の曲げ弾性率を設定 [N m2] const long EI[3] = { 1000000, 1500000, 3000000 }; //価格設定 [円/mm] const int LCost[3] = { 2,4,10 }; //梁の名前を設定 [-] const char* Name[3] = { "α","β","γ" }; //C,B,Aでの長さを設定 [mm] const int Length[3] = { 400,300,300 }; //一点荷重の大きさ [N] const int Force = 294; //解析間隔[mm] const int interval = 10; //たわみ量の拘束条件 const int limitdef = 70; //梁の設計に対してその費用を求めます int Cost(int spardesign[3]) { int result = 0; for (int i = 0; i < 3; i++) { result += Length[i] * LCost[spardesign[i]]; } return result; } //A,B,Cの順で梁の種類を受け取り、たわみ量を返します。 //通常この計算は時間がかかるのでこの関数の呼び出し回数を抑えると計算が早くなる int Deflection(int spardesign[3]) { const int N = 101; double moment[N]; double dtheta[N]; double theta[N]; double deflection[N]; //境界条件の設定 theta[0] = 0; deflection[0] = 0; for (int i = 0; i < N; i++) { //モーメントの計算 moment[i] = Force * (1000 - interval * i); //たわみ曲率(dθ)の計算 if (i <= Length[0] / interval) { dtheta[i] = moment[i] / EI[spardesign[0]]; } else if (i <= (Length[0] + Length[1]) / interval) { dtheta[i] = moment[i] / EI[spardesign[1]]; } else { dtheta[i] = moment[i] / EI[spardesign[2]]; } } for (int i = 0+1; i < N; i++) { //たわみ角の計算 theta[i] = theta[i - 1] + dtheta[i]; deflection[i] = deflection[i - 1] + interval * sin(theta[i] / 180 * M_PI); } return deflection[100]; } //flag[i][j][k]の枝切りを行います。また再帰呼び出しでに枝切りされたノードについて連鎖的におこる枝切りもおこなう void Pruning(int flag[3][3][3],int i,int j,int k) { flag[i][j][k] = 0; //パターン1. 同じ親ノードを持つ子ノードの枝切り for (int l = k+1; l < 3; l++) { flag[i][j][l] = 0; Pruning(flag, i, j, l); } //パターン2. 異なる親ノードを持つ子ノードの枝切り for (int l = j + 1; l < 3; l++) { flag[i][j][k] = 0; Pruning(flag, i, l, k); } for (int l = i + 1; l < 3; l++) { for (int m = j; m < 3; m++) { flag[l][m][k] = 0; Pruning(flag, l, m, k); } } } int main() { //A,B,Cの順にフラグをとる int flag[3][3][3]; int mincost = _CRT_INT_MAX; int mindesign[3]; //flagの初期化 for (int i = 0; i < 3; i++) { for (int j = 0; j < 3; j++) { for (int k = 0; k < 3; k++) { //最初は全部trueで格納 flag[i][j][k] = 1; } } } for (int i = 0; i < 3; i++) { for (int j = 0; j < 3; j++) { for (int k = 0; k < 3; k++) { if (flag[i][j][k]==0) { //flagが偽ならこの回は飛ばす continue; } //剛性が高い方から作ってテストしていく int spardesign[3] = { 2 - i,2 - j,2 - k }; double deflection = Deflection(spardesign); if (deflection > limitdef) { //たわみ量が70mmを上回ってしまった→コストは求めず枝切りして抜ける Pruning(flag, i, j, k); continue; } int cost = Cost(spardesign); if (mincost > cost) { mincost = cost; for (int l = 0; l < 3; l++) { mindesign[l] = spardesign[l]; } } } } } //探索終了 printf("Cost:%d,A:%s,B:%s,C:%s\n", mincost, Name[mindesign[2]], Name[mindesign[1]], Name[mindesign[0]]); for (int i = 0; i < 3; i++) { for (int j = 0; j < 3; j++) { for (int k = 0; k < 3; k++) { printf("flag[%d][%d][%d]=%d\n",i,j,k,flag[i][j][k]); } } } return 0;
図18 最適構造探索プログラムのCソースコード
このプログラムを実行すると下の結果を得られます。
Cost:5800,A:α,B:β,C:γ flag[0][0][0]=1 flag[0][0][1]=1 flag[0][0][2]=1 flag[0][1][0]=1 flag[0][1][1]=1 flag[0][1][2]=1 flag[0][2][0]=0 flag[0][2][1]=0 flag[0][2][2]=0 flag[1][0][0]=0 flag[1][0][1]=0 flag[1][0][2]=0 flag[1][1][0]=0 flag[1][1][1]=0 flag[1][1][2]=0 flag[1][2][0]=0 flag[1][2][1]=0 flag[1][2][2]=0 flag[2][0][0]=0 flag[2][0][1]=0 flag[2][0][2]=0 flag[2][1][0]=0 flag[2][1][1]=0 flag[2][1][2]=0 flag[2][2][0]=0 flag[2][2][1]=0 flag[2][2][2]=0
図19 最適構造探索プログラムの実行結果
図19実行結果のflagに注目してください。構造解析を行ったのはflagが1になっているノードのみです。実行結果からわかる通り、積極的な枝切りを行っていくことで最終的に構造解析を行ったのは27ノード中6ノードにとどまり、計算量を抑えることに成功しています。
また、計算量を削減するために、制約条件からのマージンを設定してたわみ量の大きい方の計算量を削減するという手法があります。たとえば今回の場合、たわみ量50mm以下の場合、二分探索式にノードを飛ばすといった、最初のたわみ量がある程度小さいノードを二分探索によって求めていくものです。
・実際の最適構造探索
今回は梁価格の最小化を題材に最適構造探索を行いました。実際にモノを設計する場合には、この最小・最大化パラメーターが複数存在するというケースや複数の制約条件を設けるケースが多いです。特に最小・最大化パラメーターが複数存在する際にはどのパラメーターにどれだけの重みをのせるかを表した評価関数を設けてプログラミングをしていきます。
この評価関数がいろいろ厄介で、これは多くの場合、設計者の勘にゆだねられます。最近では設計に対するフィードバッグをデータベース化し評価関数をニューラルネットワークを用いて最適化していく研究が大手メーカーを中心に行われています。
また、今回は探索木を用いて最適化を行いました。しかし、3Dプリンターを始めとする製作手法の発達により新しい最適化手法も登場し始めています。
最近話題になっているのが、トポロジー最適化です。

図20 トポロジー最適化された製品(下)[3]
これはトポロジー論をベースとした解析メソッドを持つプログラムを用いて、強度や剛性に貢献度が低い部分を肉抜きしていくもので、従来製品とは違った有機的なデザインになります。もちろん今までの製造技術では製作が困難なので、3Dプリンターを始めとするNC工作機械が用いられています。
まとめー最適構造探索アルゴリズム
・最適構造探索は様々な種類がある
・実際の設計最適を見据えるのには難儀する
さて、ここまで計算機による構造解析と最適構造探索アルゴリズムのお話をご覧いただきましたがいかがだったでしょうか。情報工学の機械工学への応用について少しでも興味を持っていただければ幸いです。
画像引用
[1]
[2]
公式集−構造計算 片持ち梁 (曲げモーメント、せん断、反力、たわみ・・)
[3]
トポロジー最適化 とぽろじーさいてきか/topology optimization - 製品設計知識
*1:むしろ今回のように線形方程式のみで求められる方が稀