1. 序文 シューティングゲームで時々見かける「曲がるレーザー」。
かっこいいですよね。これがあるだけでもゲームの見栄えがよくなると思います。 曲がるレーザーを作る方法としては, 「ベジェ曲線」を用いてレーザーの軌道を決定するやり方がメジャーなようですが, もっと簡単な方法はないのか?そんなことをなんとなく考えていたところ, レイフォースのメインプログラマーだった方が, twitterで 「レイフォースのレーザーは数式とかを使わないで非常に簡単な方法で実装しました」 という感じのことをつぶやいているのを発見しました。 レイフォースのレーザーってすごくスタイリッシュなんですけど, それが簡単に実装できるとなると, かなりうれしいですよね(プロの言う簡単がどれほど簡単かは分かりませんが)。そこで今回は, 「ベジェ曲線を用いずに曲がるレーザーを実装するためのレーザーの軌道の計算方法」を紹介しようと思います。
2. 方針 ・C++とDXライブラリを使用します。 ・レーザーは丸い弾を数珠繋ぎに発射し, それらを合成することで表現します。 ・レーザーは, 弾の速度ベクトルを1フレームごとに計算し動かします。 ・弾の速度ベクトルの向きをだんだん敵のほうに向けることで, レーザーが曲がる様子を表現します。
3. 軌道 項1で述べたように, 今回の方法では軌道を計算してトレースするのではなく, 速度ベクトルを1フレームごとに計算してレーザーを動かします。レーザーを構成する弾の速度ベクトルは, 以下のように計算します。
theta=vangle - atan2(Enemy[num].GetY()-y, Enemy[num].GetX()-x);
if (theta<-2*PI || (theta>=-PI && theta<0) || (theta>=PI && theta<2*PI)) vangle += HOMING_ANGLE;
else vangle -= HOMING_ANGLE;
vx=HOMING_V*cos(vangle);
vy=HOMING_V*sin(vangle);1行目では, 現在の弾の速度ベクトルとx軸の正方向のなす角vangleと, 弾が現在位置から一直線に標的に向かう場合の速度ベクトルとx軸の正方向のなす角との差を計算し, それをthetaとします(下図参照)。
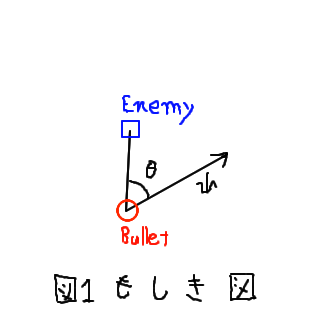
2, 3行目では, thetaの値をもとにvangleを変化させます。 thetaの絶対値がπの偶数倍に近いほど, 弾は標的に向かって進んでいるといえます。逆に, thetaの絶対値がπの奇数倍に近いほど, 標的の反対に向かっているといえます。そこで, thetaの値がπの偶数倍に近くなるようにvangleの値を少しづつ変化させていきます。
(i) theta<-2π, -π<=theta<0, π<=theta<2πのとき
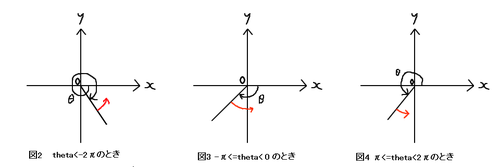
「thetaの値をπの偶数倍に近づける」ということは, 上図の半直線y=tan(theta)をx軸の正の部分に近づけることと同じことです。半直線を時計回りにまわしても, 反時計回りにまわしてもいずれはx軸の正方向と重なりますが, 上図のような場合は, 赤い矢印のようにthetaを変化させたほうが早く近づくので, vangle+=HOMING_ANGLEとします。HOMING_ANGLEは1フレームごとのvangleの変化量を表す定数で, ここでは0.2[rad]としています。
(ii) -2π<=theta<-π, 0<=theta<π, 2π<=thetaのとき
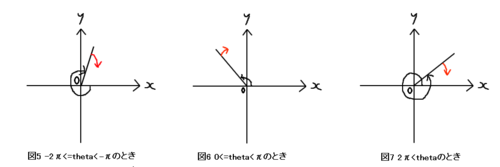
上図のようなときは, 赤い矢印のようにthetaを変化させたほうが良いので, vangle-=HOMING_ANGLEとします。それぞれ, thetaを-2π, 0, 2πに近づけていることに注意してください。
プログラムの4, 5行目では, vangleをもとに弾の速度ベクトルのx成分とy成分を計算します。HOMING_Vは, 弾の速度ベクトルの大きさを表します。
4. 実行 実行結果を以下に示します。
「レイフォース」のレーザーというよりは「ドギューン」のものに近い気がしますが, 確かにベジェ曲線を使わずに曲がるレーザーを作ることができました。しかし, 位置によってはレーザーが無駄な動きをしています。はじめ, プログラムの2, 3行目の条件式の場合分けを増やせば解決できると思い,
if (theta<-4*PI || (theta>=-3*PI && theta<-2*PI) || (theta>=-PI && theta<0) || (theta>=PI && theta<2*PI)) vangle += mul*HOMING_ANGLE;
else vangle -= mul*HOMING_ANGLE; などとしてみましたが, 敵の周囲でぐるぐる回る回数が変わるだけでした。そこで, 以下のようにプログラムを改良しました。
theta=vangle - atan2(Enemy[num].GetY()-y, Enemy[num].GetX()-x); if (theta<-2*PI || (theta>=-PI && theta<0) || (theta>=PI && theta<2*PI)) vangle += mul*HOMING_ANGLE; else vangle -= mul*HOMING_ANGLE; if(System.GetLength(x,y,Enemy[num].GetX(),Enemy[num].GetY())<100)mul*=1.1; vx=HOMING_V*cos(vangle); vy=HOMING_V*sin(vangle);
System.GetLength()は2点間の距離を計算する関数です。mulは初期値1.0の変数で, 標的との距離が100未満のとき, mul=1.1とし, フレームごとに変化させるvangleの量を+-mulHOMING_ANGLEとすることで, 弾が敵に近づくと無駄な動きをする前に敵にぶつかるようにしてしまおうという考えです。この場合の実行結果を以下に示します。標的のまわりの青い円は, 半径100の円です。この円内に入ると, mulの値が変わります。
最初の実行結果と比べて, 無駄な動きが改善されています(無駄な動きがあったほうが派手でかっこいいと思えなくもないですが)。
5. 総括 今回は「レーザーの軌道をどう計算するか」ということに焦点をあて, それ以外の具体的な実装方法については触れていません。すでにゲームをつくったことのある方なら, ここに書いたことが割りとすぐに役に立つかもしれませんが, 初心者の方は, これを読んだだけではすぐに応用できないかもしれません。しかし, シューティングゲームを作る方法を紹介している本やウェブサイトは多数存在するので, 初心者の方は分からないことを積極的に調べて, 自分だけのゲームを創ってみましょう。そしていつか, ここに書いたことが皆さんの役に立ったなら, 私はとても満足です。 また, 今回示した方法はあくまで一例に過ぎません。皆さんもいろんな方法を考えて試してみましょう。いい方法が見つかったら, こっそり私に教えてください(笑)。